Optimization Problems

In an optimization scenario, the model is known, along with the desired output (or a description of it), and the goal is to identify the input(s) that produce this output. For example, let's examine the traveling salesman problem. This seemingly abstract problem is well-known in computer science due to its many practical applications, including route organization, factory layout, production scheduling, and timetabling. In its abstract form, we are presented with a set of cities and tasked with determining the shortest route that visits each city exactly once. Given a specific instance of this problem, we possess a formula (the model) that computes the length of the tour for any sequence of cities (the inputs). The challenge is to find an input that yields a desired output, specifically a sequence of cities that results in the shortest possible length. Notably, in this example, the desired output is implicitly defined—rather than stating the exact length, we require that the tour be shorter than all alternatives, which we seek to realize.

Another example is the eight-queens problem. Here, we must position eight queens on a chessboard so that no two queens threaten each other, meaning they cannot occupy the same row, column, or diagonal. This problem can be modeled where an input represents a configuration of the queens, and the model assesses whether the queens threaten each other. The output is the count of queens that are not in a position to attack one another. Unlike the traveling salesman problem, the desired output is explicitly stated: the output must indicate that all eight queens are safe. Alternatively, a simpler model could yield a binary result, indicating "OK" or "not OK" for the overall configuration, leading us to seek an input that produces an "OK" output. This problem may not intuitively appear to be true optimization since there is no graded measure of success.

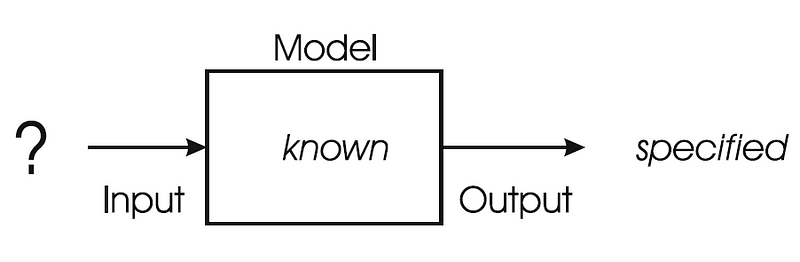
Fig. 1.1. Optimization problems frequently arise in engineering and design. The label on the output reads "specified" rather than "known," as the exact value of the optimum may not be explicitly defined, only suggested implicitly (e.g., the lowest of all possibilities).

Modelling Challenges

In a modeling or system identification context, we know corresponding sets of inputs and outputs and seek a model that accurately delivers the correct output for each input. This situation can be likened to human learning, where we strive to identify a model of the world that aligns with our previous experiences and can generalize to new situations. Take the stock market as an example, where various economic and societal indicators (like unemployment rates, gold prices, and currency exchange rates) serve as inputs, and the Dow Jones index is the output. The task here is to formulate a model that connects the known inputs to the known outputs, effectively representing this economic system.

Another example is the identification of traffic signs in images, perhaps from video feeds in a smart vehicle. The system comprises two main components: in the preprocessing stage, image processing routines analyze the electrical signals from the camera, dividing these into regions of interest that may contain traffic signs, while producing numerical descriptors of attributes like size, shape, brightness, and contrast. These descriptors represent the image digitally, and we assume that this preprocessing step is established. In the primary system, each input is a vector of numbers that describe a potential sign, with the corresponding output being a label from a predefined set (e.g., "stop," "yield," "50," etc.). The model here is an algorithm that processes images as inputs and generates traffic sign labels as outputs. The objective is to construct a model that accurately responds with the correct traffic sign labels in every circumstance. In practice, the full range of possible scenarios would be represented by an extensive collection of appropriately labeled images, and the modeling task is reduced to identifying a model that produces correct outputs for each image.

Additionally, the previously mentioned voice control system for smart homes also includes a modeling problem, where the phrases spoken by users (inputs) need to be accurately mapped to the corresponding control commands within the system.

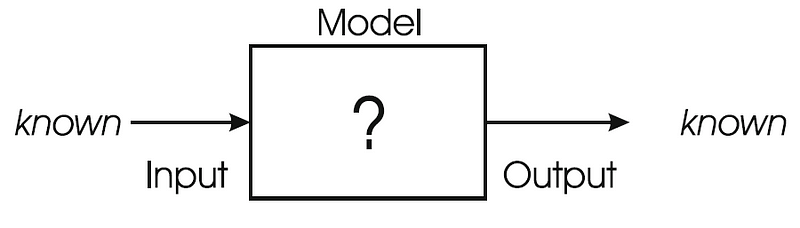
Fig. 1.2. Modelling or system identification problems are common in data mining and machine learning.

It's crucial to understand that modeling issues can be reformulated as optimization problems. The key approach is to define the model's error rate as the quantity to minimize or its accuracy rate to maximize. For instance, in the traffic sign identification challenge, we can frame it as a modeling issue: finding the correct model that accurately maps each image to the corresponding traffic sign labels. The model that resolves this problem is not known in advance, hence the question mark in the accompanying figure. To find a solution, we first choose a technology, whether it be a decision tree, an artificial neural network, or a specific programming language. This choice helps to define the necessary structure or syntax of the model. Once established, we can delineate the set of all potential solutions for our chosen technology, encompassing all valid expressions within the specified syntax. Subsequently, we can outline a related optimization problem where the input set consists of these possible models, and the output for a particular model is an integer representing how many images it correctly labeled. Clearly, a solution to this optimization problem, which maximizes the correctly labeled images, also resolves the original modeling issue.

Simulation Scenarios

In a simulation problem, we are aware of the system model and certain inputs, and our goal is to compute the corresponding outputs. Consider an electronic circuit, such as a filter designed to eliminate low frequencies from a signal. The model here consists of a complex arrangement of equations that describe the circuit's behavior. Given any input signal, this model can predict the output signal. Utilizing this model—perhaps to compare two circuit designs—proves to be far more cost-effective than physically constructing the circuit and measuring its properties.

Another illustration is a weather forecasting system, where the inputs consist of meteorological data (temperature, wind speed, humidity, rainfall, etc.), and the outputs are also those same parameters but projected into the future. The model in this case is temporal, aiming to predict meteorological conditions at later points in time.

Simulation problems manifest in various contexts, and the use of simulations provides several advantages across different applications. For example, simulation can often be more economical than evaluating real-world effects, especially for electronic circuit designers. In some cases, the real-world alternative may not even be feasible; for instance, conducting what-if analyses of different tax systems in real-time is nearly impossible. Simulation serves as a vital tool that enables us to forecast future scenarios, as seen in weather prediction systems.

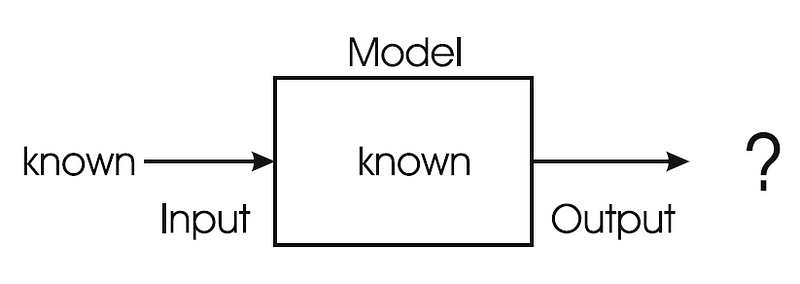
Fig. 1.3. Simulation problems frequently arise in design and socio-economic contexts.

Optimization and Simulation: A Video Introduction

To further explore these concepts, check out the following video:

This video titled "Optimization and Simulation: Introduction" provides an overview of the basic principles and challenges in these fields.

An Overview of Simulation Optimization

For a more detailed understanding of simulation optimization, watch the video below:

This video titled "An Overview of Simulation Optimization" delves deeper into the techniques and applications of optimization in simulation contexts.

In Plain English ?

Thank you for being part of the In Plain English community! Before you leave, be sure to clap and follow the writer!

Follow us on: X | LinkedIn | YouTube | Discord | Newsletter.

Discover more of our content at Stackademic, CoFeed, Venture, and Cubed.

Find additional resources at PlainEnglish.io.