Chapter 1: Introduction to Geometry Puzzles

Geometry puzzles can often appear more complex than they truly are! As someone who enjoys exploring mathematical concepts, I have become a fan of Presh Talwalkar’s Mind Your Decisions. This platform, which includes both a website and a YouTube channel, is brimming with engaging mathematical content.

Among the fascinating puzzles presented by Presh Talwalkar, one geometry challenge stands out, as it offers a clever method that simplifies the solution process. Here’s the puzzle:

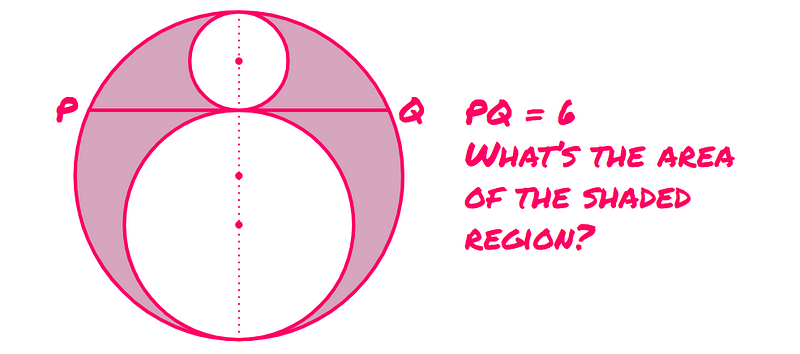
You have a large circle with a chord labeled PQ. Above and below this chord are two smaller circles that are tangent to the chord and the larger circle. Notably, these smaller circles are also tangent to one another, and the centers of all three circles are aligned. Given that PQ measures 6 units, what is the area between the two smaller circles and the larger circle, represented in [magenta]? — Presh Talwalkar (originally represented in blue)

If you find this setup puzzling, consider that the smaller circles each touch the larger circle at just one point, meet each other at a single point, and are in contact with the line PQ at one point. This configuration ensures that the centers of all three circles are collinear.

Talwalkar provides an impressive solution to this challenge, designating a and b as the radii of the smaller circles. However, there exists a more straightforward approach to arrive at the answer.

The crucial insight is that we can position the chord PQ along the diameter of the larger circle, effectively making the diameter equal to 6. This arrangement implies that the smaller circles must be the same size, each having a diameter of 3:

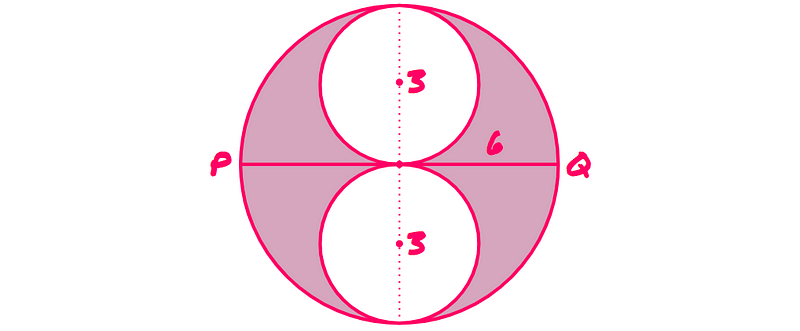
By aligning the diameter of the larger circle with the length of PQ, we simplify our calculations. The smaller circles now both have diameters of 3.

Suddenly, the problem transforms into a much simpler task! The shaded area can be determined by subtracting the areas of the smaller circles from the area of the larger circle. Recall the formula for the area of a circle:

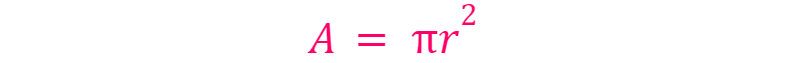
Here, A represents the area of the circle, and r denotes the radius. The radius of the larger circle is calculated as 6/2 = 3, while each smaller circle has a radius of 3/2 = 1.5. Thus, we can compute the shaded area as follows:

This method yields the same result that Talwalkar arrived at.

Thank you for reading! If you're interested in supporting Street Science, please consider contributing on Patreon.

Chapter 2: Video Insights on Geometry Puzzles

In the video titled "A Quick Geometry Puzzle," viewers are guided through the thought process behind solving a similar puzzle. The explanations provided can enhance your understanding and approach to geometry challenges.

The second video, "A Quick and Easy Geometry Puzzle Solved in Two Ways," showcases different methods to tackle geometry puzzles, emphasizing the versatility in problem-solving strategies.