Exploring Delta Warp: Journey Through the Cosmos
Written on
Chapter 1: Introduction to Delta Warp
Delta Warp has often been discussed in the context of its capability to bridge vast distances between worlds. However, its role in fostering connections among different civilizations across the galaxy is less frequently highlighted.
Essentially, Delta Warp refers to a technology that enables the formation of Einstein-Rosen Bridges, commonly known as "wormholes," linking two distinct locations in space. These locations can be viewed as parallel dimensions with no intervening space. Anything that enters one end of the wormhole will instantly appear at the other end. The Delta Warp drive can generate a series of sequential wormholes along an interstellar vessel's trajectory, significantly minimizing the space that needs to be covered and rendering non-relativistic interstellar travel not only feasible but also quite enjoyable.

Chapter 2: Calculating Travel Time
In this section, we will delve into the calculations necessary to estimate the duration of interstellar journeys. This will enhance the realism of your game and provide your characters with opportunities for interaction beyond the challenges of combat and exploration.
Section 2.1: Steps to Calculate Travel Duration
To determine the time required for any interstellar journey, follow these steps:
- Determine the Voyage Distance: Select the X, Y, and Z coordinates for both the originating and destination stars (measured in light-years).
- Identify the Maximum Velocity (VelocityMax): This information may not be readily available in the spacecraft's description; refer to the guidelines below for assistance.
- Calculate the DeltaRatio: This is based on the CoreMass effect detailed later. The standard DeltaRatio is 1.39 x 10??.
- Calculate Time in Delta-Warp: This is the ratio of space between the warp holes to their lengths (DeltaRatio) multiplied by the journey's length in meters (distance) divided by the spacecraft's maximum sustainable speed (VelocityMax). The outcome will be in seconds; to convert to days, hours, and minutes, divide by 60 twice to get minutes and hours, and then by 24 for days.
To account for acceleration and deceleration, divide VelocityMax by the G-forces the ship can withstand (+1), then multiply by 4.
Example: If the pilot of an Andromadeian Class vessel wishes to travel from Earth to Alpha Centauri, and after reaching the ship’s maximum velocity of 30,000 m/s, engages the D-Warp drive, the power plant would yield a DeltaRatio of 1.39 x 10??. The distance is 4.6 light-years, and the ship is equipped with 9G inertial dampeners.
Time in D-Warp:
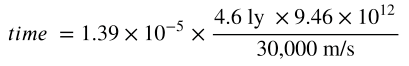
= 2016 seconds, or approximately 5.6 hours.
Time for Acceleration and Deceleration:
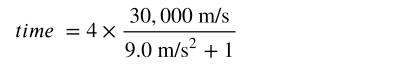
= 3.3 hours.
Total Journey Time: The one-way trip from Earth to Alpha Centauri takes about 8.9 hours, with the return journey requiring an additional 8.9 hours.
Section 2.2: Core Mass and DeltaRatio
Several factors influence the DeltaRatio, including the power output (P) of the average ship, typically around 60MW, and the mass (M) of the average D-Warp core, which is about 10 kg.
- P: Power output of your ship in MW
- P ª: Standard power output of 120MW
- M: Mass of the ship's drive in kg
- Mª: Standard drive core mass of 20 kg
The calculation is as follows:
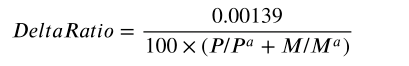
Caution: If the DeltaRatio exceeds 1.39 x 10??, the DeltaWarp process may create a "fizzing" effect, leading the drive to become supercritical, resulting in a mini-black hole, followed by a rapid implosion and explosion—a phenomenon colloquially known as a "crunch."
Typical VelocityMax for Spacecraft:
- Older or larger vessels (High-liners) have slower Vmax = 1,000–5,000 m/s.
- Newer, smaller vessels have a moderate Vmax = 5,000–10,000 m/s.
- Fast, small crafts can reach Vmax = 10,000–20,000 m/s.
- Ultra-small, speed-oriented crafts achieve Vmax = 20,000–30,000 m/s.
Chapter 3: Additional Resources
In this video titled "Neo Geo Pocket - Delta Warp," viewers can explore the intricacies of Delta Warp, including its mechanics and implications for gameplay.
The second video, "[TAS] NGP Delta Warp by callumbal in 39:23.95," provides a thorough demonstration of the Delta Warp technology in action within a gaming context.