Exploring the Intersection of Algebra and Quantum Mechanics
Written on
Chapter 1: The Synergy of Linear Algebra and Quantum Mechanics
Quantum mechanics can often be interpreted as an application of linear algebra within function spaces. In this realm, we encounter concepts such as vector spaces, bases, base transformations, and linear transformations—ideas that closely resemble the terminology used in quantum mechanics. The connection can be summarized as follows:
- Vector spaces correspond to Hilbert spaces in quantum mechanics, which are essentially function spaces that interact harmoniously.
- In this framework, linear transformations take the form of operators.
- Bases serve as fundamental elements of these spaces, typically represented by the eigenvalues of operators.
- Transformations between bases can be likened to transitioning between momentum and position in quantum mechanics.
A practical illustration of these concepts arises when calculating the propagator. While I won't delve into the entire computation for the sake of brevity, it's essential to keep these principles in mind as we explore the problem described below.

Computing a Propagator with Linear Algebra Principles
In quantum mechanics, the propagator provides insight into how a quantum state transitions over time. While path integrals are the conventional method for calculating the propagator, there are more straightforward approaches available. The propagator can be expressed as follows: the state with position eigenvalue (p) evolves over time, with the amplitude indicating the likelihood of reaching the state with position eigenvalue (q).
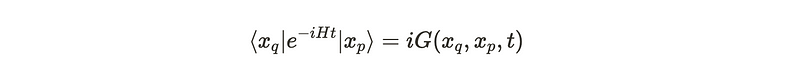
In a free space scenario—characterized by the absence of potential—the Hamiltonian can be represented by the function below. At first glance, this expression appears logical as it reflects the kinetic energy of a particle in classical mechanics. Notably, (p) here is not a mere variable but an operator that acts upon states. Currently, our understanding is limited to its action on momentum states corresponding to a specific momentum (p), simply scaling these states by their actual momentum. This scaling is depicted on the right side.
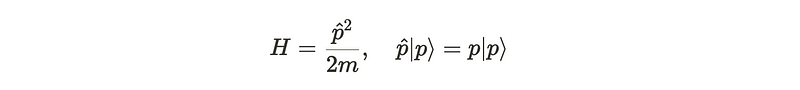
Determining the exact value of the propagator can be quite challenging. Fortunately, we can employ some mathematical techniques to facilitate this process. In the scenario described, the Hamiltonian operates on momentum states, while the states in our propagator are defined in position space. Therefore, a change of basis is necessary to express position operators in momentum terms. We achieve this through a Fourier transform, expressing the position states as a summation of various momentum states:

This insight simplifies our calculations considerably. By substituting this expansion into the propagator's expression, we can apply the momentum operator to the states and then factor out the expression situated between the momentum states. Notably, the expression is only non-zero when (p' = p), given the orthogonality of momentum states.
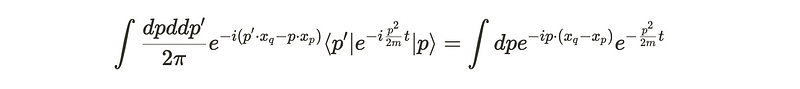
At this point, we've largely completed our task! The final step involves evaluating the Gaussian integral on the right side by completing the square. I encourage readers to continue this exercise independently, leading to the outcome:
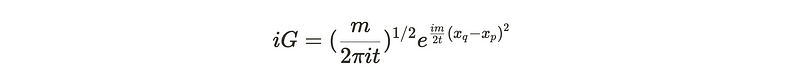
Chapter 2: Understanding Linear Algebra in Quantum Contexts
In this video titled "Ch 1: Why linear algebra? | Maths of Quantum Mechanics," the speaker explores the significance of linear algebra within the framework of quantum mechanics and its foundational role in understanding quantum systems.
The second video, "Algebraic Techniques for Dealing with Difficult Operators in Quantum Chemistry on a Quantum Computer," delves into advanced algebraic methods for managing complex operators in quantum chemistry, specifically in the context of quantum computing.