Unraveling Euler's Insights on Odd Perfect Numbers
Written on
Chapter 1: The Intrigue of Perfect Numbers
Perfect numbers have captivated mathematicians for centuries. The concept is straightforward: for any given number, identify its divisors (excluding the number itself). For instance, the divisors of 6 include 1, 2, and 3. Adding these divisors together, we find that 1 + 2 + 3 = 6, demonstrating that 6 is indeed a perfect number.
As we delve deeper, we will examine the complete sum-of-divisors function, denoted as ?(N), which includes N itself. A number N is classified as perfect if ?(N) equals 2N. However, perfect numbers are rare; in fact, 6 is the smallest perfect number, with 28 being the next. Despite a wealth of research on the nature of perfect numbers, two fundamental questions remain unanswered:
- Are there infinitely many perfect numbers?
- Do odd perfect numbers exist?
Solving either of these questions could bring you significant recognition. They appear deceptively simple yet have thwarted numerous attempts at proof or counterexample throughout history.
Rather than exploring the first question, I find it particularly fascinating that Euler established that any odd perfect number must conform to a specific structure back in the 1700s, yet we still do not know if such numbers exist! Presently, computational checks have been performed up to around 10¹⁵ without discovering any odd perfect numbers. Recent advancements in research on odd perfect numbers have emerged as recently as this year, indicating that this area remains vibrant and full of potential.
Next, we'll explore Euler's elementary proof regarding the structure of odd perfect integers, and perhaps one of you will solve this enduring mystery.
Section 1.1: The Form of Odd Perfect Numbers
Despite our ignorance regarding the existence of odd perfect numbers, the form they must take has been understood for centuries. The theorem asserts: If N is an odd perfect number, then it can be expressed as:

Here, p represents a prime number of the form p = 4n + 1 and does not divide Q. In essence, an odd perfect number must be a perfect square multiplied by a specific type of prime number raised to a particular power (1, 5, 9, …).
To illustrate, if n equals 1, then p would be 5. If Q equals 3, then the perfect square is 9, making N equal to 45. The divisors of 45—1, 3, 5, 9, and 15—sum to 33, confirming that 45 is not a perfect number. While this theorem does not yield actual odd perfect numbers, it provides insight into the characteristics they must possess.
The proof of this theorem is elementary, relying on the thoughtful examination of even and odd integers and exploring all possible cases. Despite its simplicity, it can be challenging to follow since it requires keeping track of numerous variables simultaneously.
Video Title: Perfect Number Proof - Numberphile - YouTube
This video provides a captivating overview of perfect numbers, illustrating their unique properties and the fascination they hold for mathematicians.
Section 1.2: Preliminary Concepts
Before we embark on the proof, let's clarify the definitions of even and odd numbers. A number x is odd if it can be expressed as x = 2k + 1 for some integer k, while a number x is even if it can be represented as x = 2k for some integer k.
Fact 1: The sum of two odd numbers is always even.
Fact 2: The sum of an odd number and an even number is always odd.
Fact 3: The divisors of pⁿ, where p is prime, are 1, p, p², …, pⁿ.
Fact 4: The sum of divisors of pⁿ (notated ?(pⁿ)) is even if n is odd.
Fact 5: The sum of divisors is weakly multiplicative, meaning if N and M share no common prime factors, then ?(NM) = ?(N)?(M).
For example, if we take N = 3 and M = 5:
?(15) = 1 + 3 + 5 + 15 = (1 + 3)(1 + 5) = ?(3)?(5)
Now, let's proceed to prove Euler's form of odd perfect numbers.
Chapter 2: Proving Euler’s Theorem
Let N represent an odd perfect integer. Utilizing the Fundamental Theorem of Arithmetic, we can factor N into its unique prime factorization:
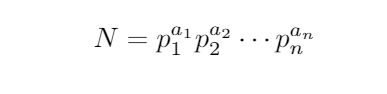
As N is odd, none of its prime factors include 2. Since N is a perfect number, we know that ?(N) = 2N. We will apply the definition alongside the previously discussed facts to derive a crucial equation.

A significant insight arises: only one of the factors can be even. If two factors were even, we could factor out 4, which leads to a contradiction. Therefore, all other factors must be odd. This indicates that all but one of the a? in the prime factorization of N are even.
Consequently, we can express N as p?Q², where Q is odd, and p does not divide Q. Assuming p = 4b + 3 for some integer b, we observe that ?(p?) = (1 + p)(1 + p² + … + pⁿ⁻¹). Since 1 + p divides ?(p?), this must also divide 2N, which leads us to a contradiction.
Thus, the only possibility remaining is that p must have the form 4b + 1, confirming our initial claim.
Video Title: How Mersenne Primes Generate Perfect Numbers - YouTube
This informative video delves into the relationship between Mersenne primes and perfect numbers, providing a deeper understanding of these mathematical concepts.
Final Thoughts on Odd Perfect Numbers
Numerous findings have emerged since Euler's theorem was established. In 1980, Hagis demonstrated that an odd perfect number must possess at least eight distinct prime factors. In 2005, Hare expanded this finding, asserting that it must include at least 75 (not necessarily distinct) factors. More recently, in 2012, Ochem and Rao proved that odd perfect numbers must have at least 101 factors.
Various results regarding the size of factors have also been established, but the structural properties of odd perfect numbers remain a more intriguing area of research. There exists a plethora of results concerning the exponents that can occur and the congruence relations involving N.
If you're seeking a longstanding problem to explore, consider investigating odd perfect numbers. If you can determine a guaranteed form for an odd perfect number that contradicts the established theorem, you could conclusively prove that none exist—a feat that could secure your place in mathematical history.
For now, computational checks will continue as we await new insights.