Chapter 1: Introduction to Game Theory

This chapter marks the third installment in our exploration of Game Theory. For those interested, you can find the previous chapters linked here: Chapter I and Chapter II.

In our last discussion, we delved into zero-sum games—situations like Tic-tac-toe where one player's victory directly translates to the other player's loss. However, many scenarios in real life fall outside this category. One notable example is the classic Prisoner’s Dilemma.

Imagine you and an accomplice are apprehended by law enforcement. The authorities possess sufficient evidence to convict both of you for a lesser crime, which would result in a one-year prison sentence. Yet, they aim to impose a harsher penalty for a more serious offense, such as bank robbery, which carries a four-year sentence. Unfortunately, they lack enough evidence to proceed unless you both decide to testify against one another. You and your partner, however, have agreed to remain silent.

After some deliberation, the detectives devise a plan. They place you both in separate interrogation rooms, completely isolating you from each other. Each of you is then presented with a choice: if you betray your partner, you will avoid conviction for the burglary. Conversely, if your partner chooses to betray you, you will face charges for the bank robbery. The question is, what should you do to minimize your time behind bars?

To break down the situation, consider the following four potential outcomes:

1. Both you and your partner remain silent. In this case, you both receive a one-year sentence for the burglary, but not for the robbery.
2. If you betray your partner while they remain silent, your partner faces a total of five years (one for burglary and four for robbery), while you walk free.
3. If you choose to stay silent and your partner betrays you, you receive five years, and they go free.
4. If both of you betray each other, you each receive four years in prison for the robbery, but neither of you gets convicted for the burglary.

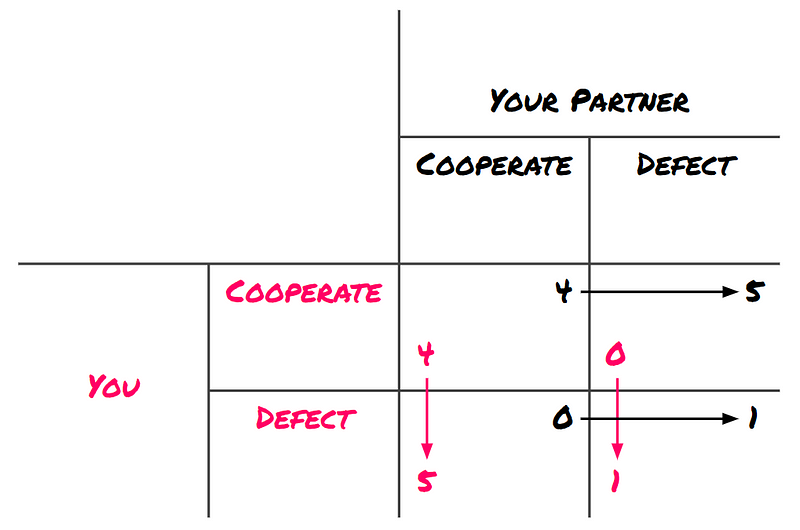
To illustrate this in terms of utility (where more is preferable), the situation can be summarized as follows:

In this context, cooperating means remaining silent, while defecting means betraying your partner. This scenario is a clear example of a non-zero-sum game; one player's gain does not necessarily equal another's loss. Transitioning from both players defecting to both cooperating yields a combined increase of three utility points.

It is noteworthy that while defecting offers the highest utility when your partner cooperates, the unknowns surrounding their choice complicate matters. If your partner does cooperate, choosing to defect provides five utility points, whereas cooperating yields only four. Conversely, if your partner defects, defecting yields one utility point compared to zero for cooperating. Therefore, defecting emerges as the superior strategy regardless of your partner's actions.

Consequently, defecting becomes the dominant strategy for both players. This implies that both players will likely choose to defect, resulting in only one utility point for each, equating to four years in prison. This outcome signifies a significant loss of potential utility.

What is particularly interesting about this scenario is that when both players follow their dominant strategy, they find themselves in a state known as Nash Equilibrium. This situation occurs when no player can improve their outcome by altering their strategy while the other player maintains theirs.

Given that your partner chooses to defect, your optimal move is to do the same. Likewise, your partner’s best choice, knowing you will defect, is to defect as well:

While the ideal outcome appears to be mutual cooperation, it is a disappointing mathematical reality that the Nash Equilibrium doesn't always align with this optimal solution. More precisely, a Nash Equilibrium isn't guaranteed to be Pareto Efficient. Further details on this concept will be covered in the next chapter.

If you appreciate the insights provided by Street Science, consider supporting us on Patreon.