Understanding the Essence of Derivatives: A Comprehensive Guide
Written on
Chapter 1: Introduction to Derivatives
Derivatives are a concept that most of us have encountered at some stage. There are numerous definitions available online, such as describing it as the slope of a tangent line to a function's graph or as the "instantaneous rate of change." While these definitions aren't wrong, they fail to encapsulate the true essence of derivatives and the genius of the mathematicians who developed them.
To truly grasp this concept, we need to revisit the fundamentals. In mathematics, functions model how one quantity, whether physical or abstract, relates to another. For instance, consider the following function.

Gravitational Force Between Two Masses
The function ( F ) represents the gravitational force between two masses at a distance ( r ). Here, ( F ) is the dependent variable, while ( r ) is the independent variable. The values that ( r ) takes influence the values of ( F ). Thus, we can express the gravitational force as a function of distance: ( F = F(r) ).
To simplify our exploration, let’s consider a basic function: ( f(x) = x^2 ). This could represent a force or any other quantity we choose.
At this point, an important question arises. We’ve established that a function is a quantity dependent on another. However, the function’s formula does not convey how sensitive this dependence is. Referring back to our gravitational function ( F = F(r) ), although we have a formula for gravitational force, it does not indicate how changes in the distance ( r ) affect ( F ). Specifically, if we slightly alter ( r ), how much will ( F ) change? This inquiry led to the birth of the derivative concept.
The derivative of a function ( f = f(x) ) reveals how quickly ( f(x) ) alters when we make a tiny adjustment to ( x ). If ( df ) signifies a minor change in ( f(x) ) and ( dx ) denotes a minor change in ( x ), then the derivative acts as the proportionality factor.
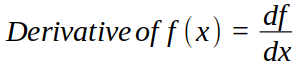
Applications of Derivatives
Derivatives are central to both mathematics and physics, making it challenging to envision these fields without them. We will now delve into their various applications and understand why they are not only essential but also logical.

The Contributions of Newton and Leibniz
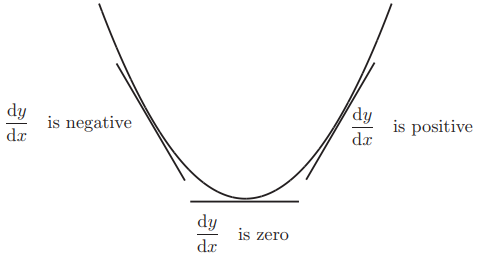
Isaac Newton and Gottfried Wilhelm Leibniz are credited with independently formulating the principles of infinitesimal calculus. In mathematics, one straightforward application of derivatives is in determining whether a function is increasing or decreasing. Based on our earlier definition, if a function’s derivative ( f'(x) ) is positive, the function is increasing; conversely, if it is negative, the function is decreasing.
What matters here is not the intricate mathematics but the intuition behind it. If we make a small change ( dx ) to ( x ) and the resulting change ( df ) in ( f(x) ) is positive, it indicates that ( f ) is increasing. The reverse applies for decreasing functions, highlighting the simplicity of this concept.
Derivatives also help identify the minimum and maximum values of a function. At a function’s maximum, the derivative must equal zero, meaning that when ( df = 0 ), the function attains its extremum since changes in the independent variable no longer affect the dependent variable.
Chapter 2: The Role of Derivatives in Physics
Derivatives are equally crucial in physics. Before we explore further, let’s clarify the relationships between position, velocity, and acceleration—concepts familiar even to non-scientists.
Defining Velocity
How might a layperson define velocity? It could be described as the distance traveled by an object divided by the time taken, which only gives an average speed. However, we aim to define instantaneous velocity—the speed and direction of an object at every moment.
In physics, velocity is naturally defined as the derivative of an object's position. It is the ratio of a small change in position to a small change in time. So, what about acceleration? Acceleration is defined as the derivative of velocity! This example illustrates the simplicity and power inherent in the derivative concept.
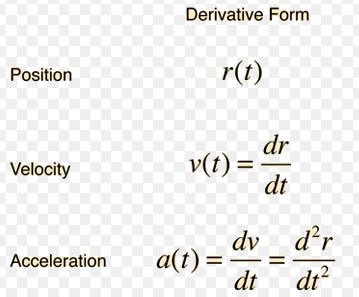
The Essence of Derivatives in Physics
Generally, the derivative epitomizes the essence of physics, as it allows us to study how the change of one physical quantity influences others. This is why derivatives are integral in various fields of physics, including classical mechanics, electrodynamics, quantum mechanics, and relativity.
Some fundamental equations that include derivatives are:
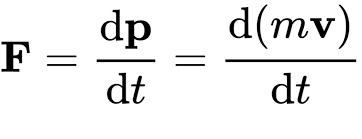
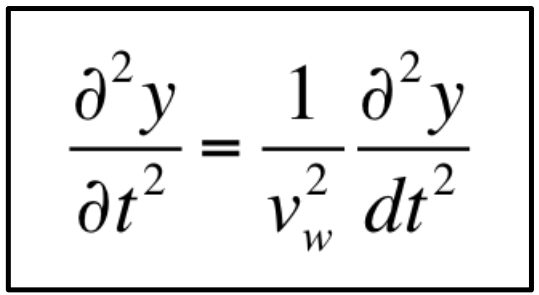
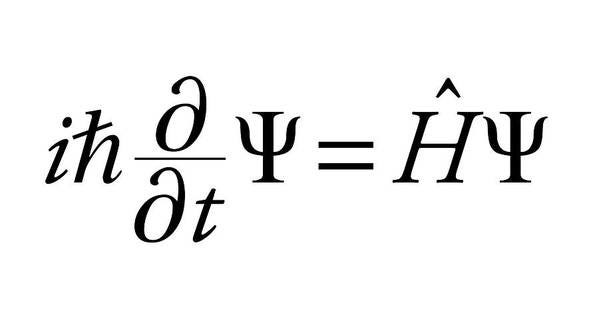
These equations represent some of the foundational principles in physics. Rather than focusing on exact measurements, physics is concerned with change and the dynamic nature of the universe. The concept of derivatives is key to understanding this complexity and the various phenomena it encompasses.
In this video titled "Calculus I: Derivative Intuition, Definition, and Applications," viewers will gain insight into the fundamental concepts of derivatives, their definitions, and practical applications in various fields.
The video "The Intuitive Concept of a Derivative" provides a deeper understanding of how derivatives function and their significance in both mathematics and physics.