Chapter 1: Introduction to the 1996 Integral Problem

The integral presented in the International Mathematical Competition of 1996 is a noteworthy challenge for undergraduate students. This competition serves as a counterpart to the International Mathematical Olympiad, yet it tends to focus on more advanced material. Despite its complexity, clever strategies can simplify the problem, sometimes allowing for high school-level methods to be effective. Before delving into the solution, it's advisable to attempt the problem yourself; you might surprise yourself with how far you can progress! Here, ( n ) denotes a natural number.

We begin by examining the limits of integration. The upper and lower limits appear to be identical, apart from a negative sign. However, our integrand does not exhibit odd or even properties, thus negating any immediate cancellation. A viable approach is to express the integrand as a combination of even and odd functions. The rationale behind this is that the odd function will negate itself, leaving only the even function. There are two primary methods to achieve this.

One method is to express the integrand as ( f(x) = g(x) + h(x) ), where ( g ) is an odd function and ( h ) is even. We can then use the relation ( f(-x) = -g(x) + h(x) ) to solve for ( g ) and ( h ) using simultaneous equations. Alternatively, a more straightforward approach involves using the substitution ( u = -x ) and adding the two resulting integrals. In this case, the even component remains unchanged while the odd component cancels out, effectively yielding double the even component. We illustrate this process below:

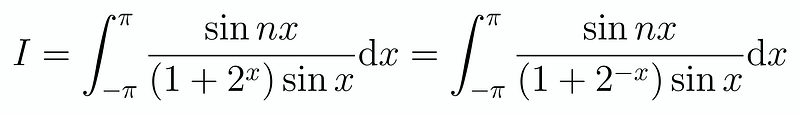
Notice the alteration in the exponent within the denominator. We can now combine these integrals to arrive at the following expression:

By simplifying and canceling terms, we are left with a much more manageable integral, which is expressed as:

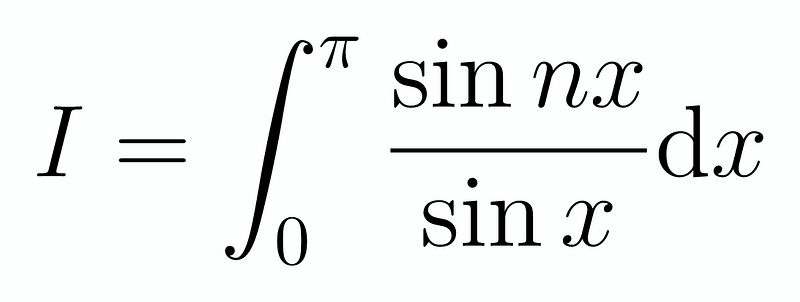
This integral is highly regarded in mathematical circles and has been addressed in previous discussions. The solution we derived previously was:

Were you able to solve the problem? Did you adopt a different approach? Share your thoughts in the comments below.

If you enjoyed this article or have suggestions for future problems, please consider supporting my work.

Chapter 2: Video Solutions and Insights

Explore the 1996 William Lowell Putnam Mathematical Competition, problem B4, and its solutions.

Review the techniques and solutions for the 2008 William Lowell Putnam Mathematical Competition, problem A4.