The Renaissance Era and Practical Applications

During the Renaissance, mathematicians began to move away from the ancient focus on perfection. They started applying mathematical reasoning to real-life situations, leading to groundbreaking work in probability by Blaise Pascal and Pierre de Fermat in the 17th century. Their studies began with the analysis of dice rolls, which, interestingly, are shaped like the ideal Platonic Solids.

This shift toward probability marked a significant mental transition. Rather than merely exploring unchanging forms, mathematicians focused on predicting the outcomes of uncertain events. Since future events are inherently unpredictable, their work required developing well-reasoned estimates for the most likely outcomes. Although we can't predict results with certainty, mathematics can help us understand the distribution of possible outcomes.

Build Mathematical Reasoning with Number Proofs

This video delves into the fundamentals of mathematical reasoning, providing insights into number proofs and their application in problem-solving.

Understanding Basic Probability

Consider a fair six-sided die, where each face has an equal chance of landing face up. The probability of any single outcome is 1/6, leading to the distribution shown below.

Each possible outcome has an equal probability of approximately 0.166. While this might seem straightforward, let's increase the complexity by rolling two six-sided dice and summing the results. The possible outcomes range from two to twelve, and Pascal and Fermat developed a table to analyze this scenario.

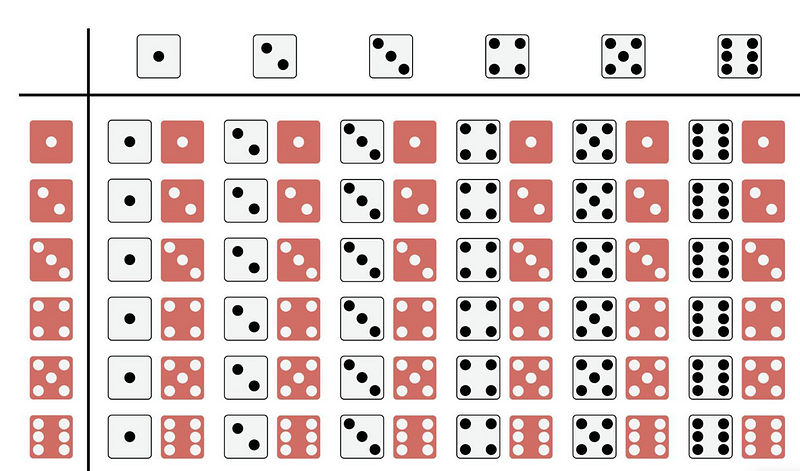
This table reveals the 36 potential combinations of rolls. Notably, some totals, like two, appear only once, while seven occurs six times. Such insights are invaluable, particularly for players of games like Settlers of Catan.

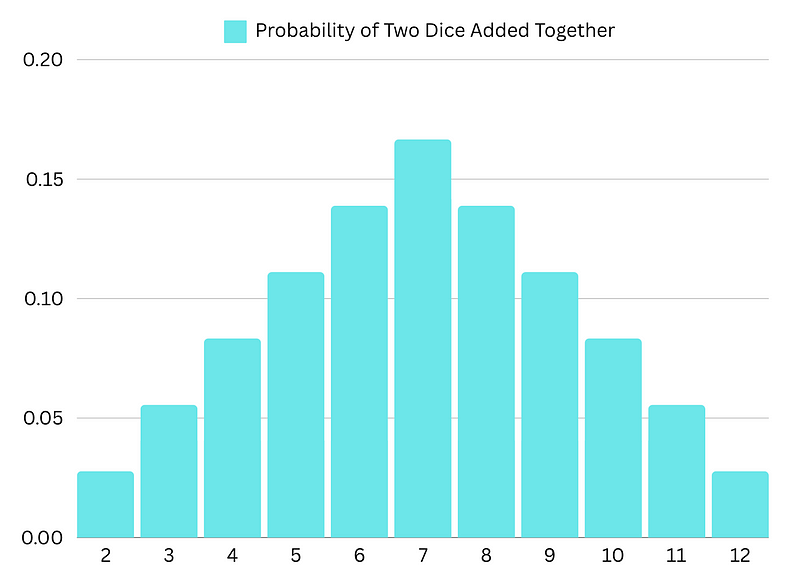
The study of probability has since evolved, with a greater focus on understanding distributions rather than precise results. One of the most significant advancements in this field is Bayes’ Theorem.

Bayes' Theorem: A Breakthrough in Probability

To make informed decisions, it's essential to adjust our understanding based on new information. Sticking to outdated assumptions is a common pitfall in decision-making. Thomas Bayes made a considerable contribution in the 18th century by formulating a mathematical method to revise reasoning upon acquiring new evidence. Let’s explore a simple example of its application.

Imagine we want to predict whether it will rain based on the presence of clouds in the morning. We know that it rains 25% of the time, clouds are present in the morning 15% of the time, and when it rains, there is a 50% chance of clouds being present.

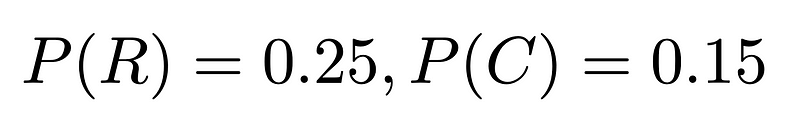
To express this mathematically, we denote the probability of rain on any day as P(R) = 0.25 and the probability of clouds in the morning as P(C) = 0.15. The relevant conditional probability, P(C|R), indicates that if it rains, there is a 50% chance of clouds in the morning.

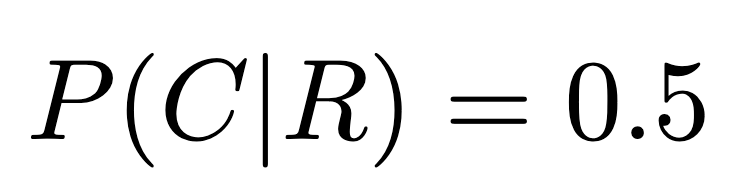
However, our goal is to determine P(R|C), the probability of rain given the presence of clouds. Bayes’ Theorem allows us to calculate this.

Upon calculation, we find that P(R|C) = 83.3%. This indicates that if clouds are present in the morning, the likelihood of rain increases significantly. Conversely, if there are no clouds, the probability drops to just 3.7%.

This may seem surprising at first—why is P(R|C) so much higher than P(C|R)? The answer lies in the relationship between the two events. Rain is relatively common, while morning clouds are less frequent. Therefore, when clouds do appear, it str