Chapter 1: Introduction to Quantum Computing Mathematics

In order to embark on your journey into quantum computing, a solid understanding of mathematics is essential. This guide will highlight the crucial mathematical skills you need, with a focus on trigonometry, which is foundational in the field.

Source: Jason Koxvold, Wired.co.uk

For additional insights, explore the rest of this series:

• All The Math That You Need To Start Doing Quantum Computing (Part-I)
• Easy Lessons for An Absolute Beginner to Quantum Computing
• All The Math That You Need To Start Doing Quantum Computing (Part 3)
• Easy Lessons for An Absolute Beginner to Quantum Computing

You may also want to check out my publications:

• The No Bulls**t Guide To Learning Python
• The No Bulls**t Guide To Learning Artificial Intelligence

Chapter 2: Trigonometry Basics

Trigonometric functions reveal the connections between angles and the ratios of the sides of right triangles. Take a look at the representation of a right triangle below:

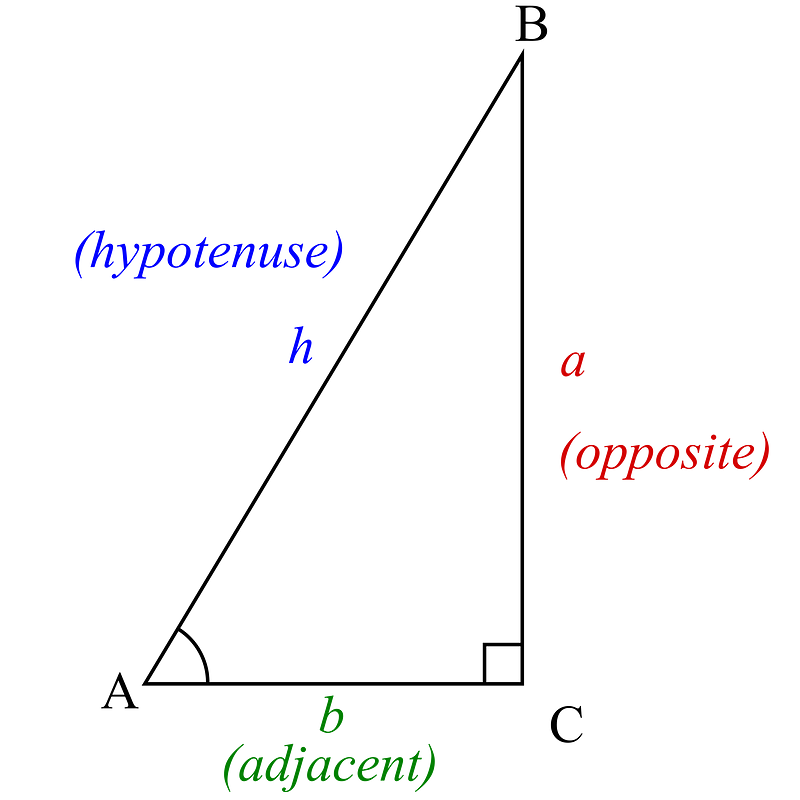
This triangle illustrates the primary trigonometric functions:

The reciprocals of these functions are:

The mnemonic SOH-CAH-TOA can help you remember these ratios:

• Sine = Opposite ÷ Hypotenuse
• Cosine = Adjacent ÷ Hypotenuse
• Tangent = Opposite ÷ Adjacent

Chapter 3: Trigonometric Graphs

The graph of sin(x) is depicted below:

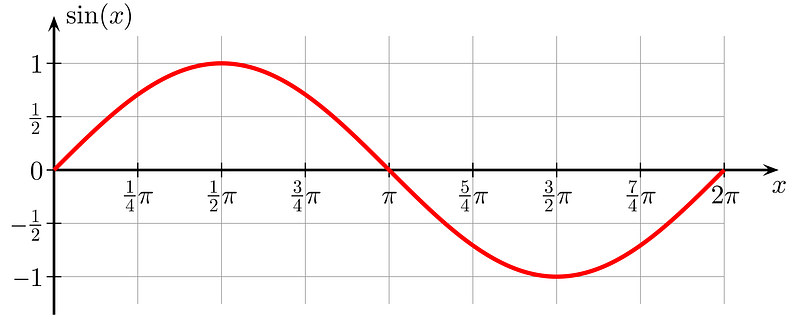
Image from Wikipedia By Geek3

Next, we see the graph of cos(x):

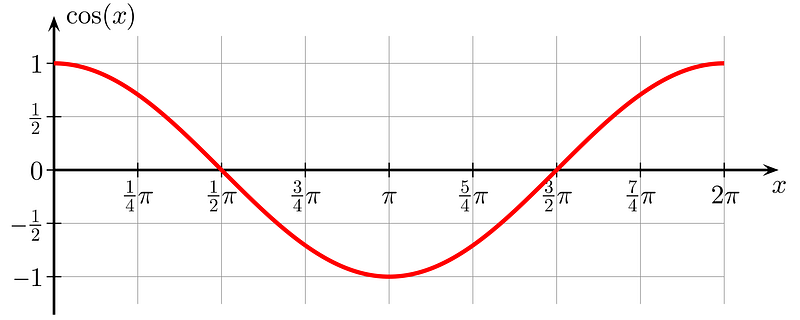
Image from Wikipedia by Geek3

Notably, sin(x) and cos(x) exhibit a phase difference of π/2. This means that shifting the cos(x) curve by π/2 aligns both graphs.

The graph of tan(x) is represented as follows:

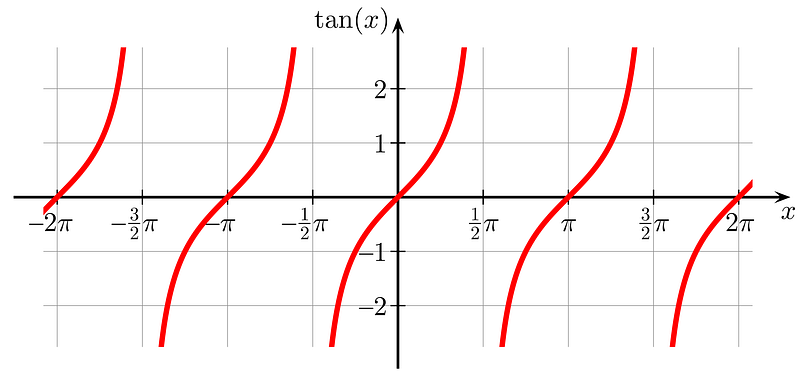
Image from Wikipedia by Geek3

Chapter 4: Calculating Trigonometric Values

If you inscribe a right triangle within a circle with a radius of one, the point where the radius meets the circle's circumference can be represented by coordinates (x, y):

• x = cos(θ)
• y = sin(θ)

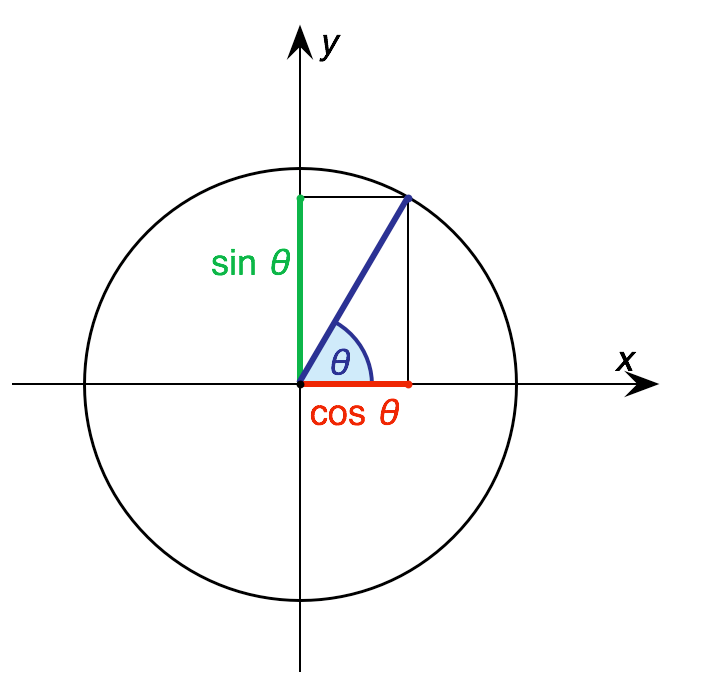
You can derive values for different angles (θ) by constructing a triangle within a circle and analyzing its ratios.

Chapter 5: Understanding Radians

Angles are often measured in radians, where one radian corresponds to the angle subtended at the center of a circle by an arc that is equal to the circle's radius.

Key radian conversions include:

• 2π radians = 360°
• 1 radian = 57.2958°

Chapter 6: Exploring Trigonometric Identities

The following identities represent the Pythagorean theorem in a different format:

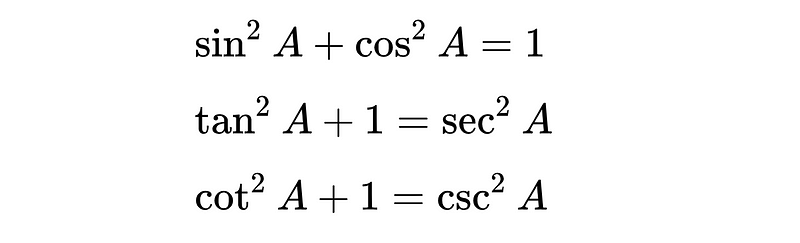
Furthermore, the identities below illustrate Euler’s formula:

If an angle θ can be expressed as the sum or difference of two angles α and β, represented as θ = α ± β:

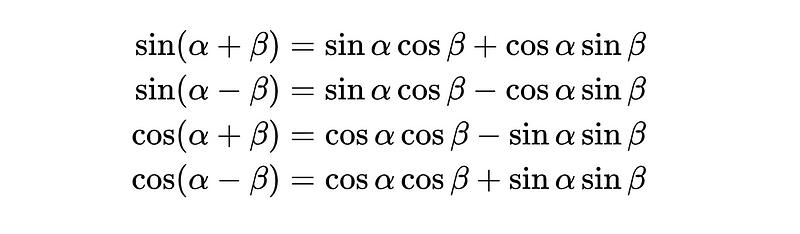
The first video, "Math Skills You Need for Quantum Computing," offers an overview of essential mathematical skills necessary for diving into quantum computing.

The second video, "The Math of Quantum Computing," elaborates on the mathematical principles underpinning quantum mechanics.

Conclusion

This concludes our exploration of the mathematical foundations required for quantum computing. Thank you for your attention, and I hope you found this guide helpful!